Понятие сингонии и осей природных кристаллов
Кристаллография - учение о кристаллах - необходима для диагностики минералов и их агрегатов. Часто минералы встречаются в природе в виде правильных кристаллов, выросших в подземных пустотах, но гораздо чаще встречаются в виде сплошных зернистых или плотных образований. Минералы, кристаллизовавшиеся в условиях земной коры, образованы по определенным законам. Их кристаллографическая форма зависит от химического состава, а также от физических условий образования - давления и температуры. Иногда только по форме и цвету кристаллов сразу можно определить минерал. В отечественной литературе употребляется термин "сингония" для описания формы кристаллов и положения его осей, поэтому мы и будем использовать его в дальнейшем.
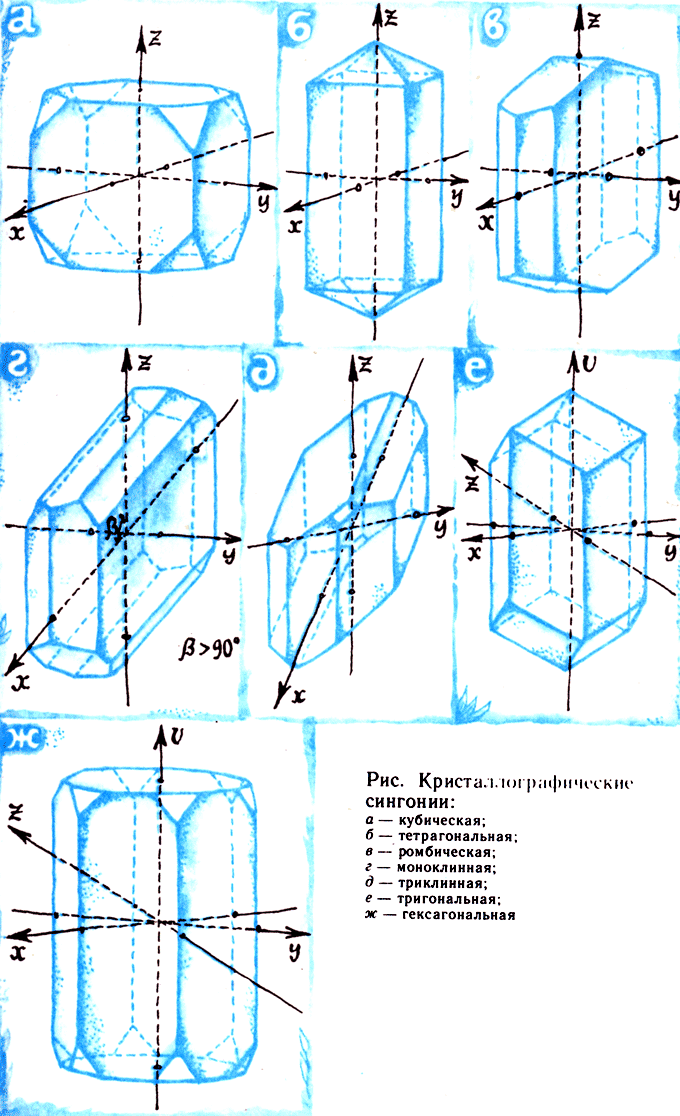
Попробуем мысленно собрать вместе разные кристаллы и посмотрим, как их можно классифицировать по форме в целом. Это поможет нам уяснить некоторые термины и обозначения, которые часто встречаются в книгах по минералогии. Расположим кристаллы так, чтобы ось симметрии наибольшего порядка, или главная призма, или группа параллельных ребер были направлены по вертикали. В центре каждого кристалла построим систему координат, условившись проводить координатные оси параллельно главнейшим ребрам кристалла, осям и плоскостям симметрии. Сравнивая теперь кристаллы, мы увидим значительные различия во взаимном расположении координатных осей и в том, как развиты кристаллы в направлении каждой из них. Это позволит нам разделить все кристаллы на семь кристаллографических сингоний.
Для графических построений и в классификационных целях минералоги и кристаллографы используют кристаллографические оси и осевые системы. В зависимости от длины отрезков, отсекаемых на кристаллографических осях, и взаимного расположения этих осей различают семь осевых систем.
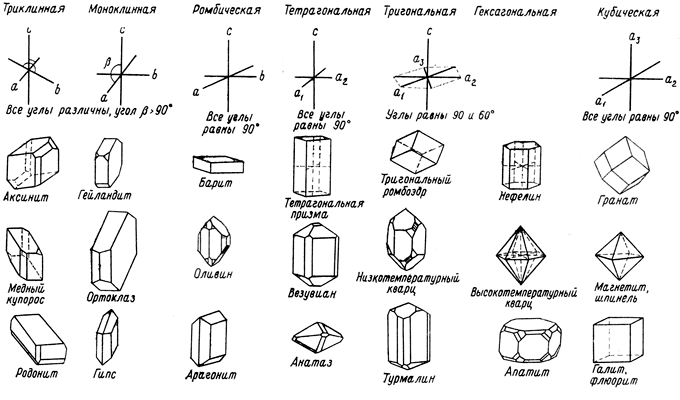
Кубическая сингония. Три равновеликие оси пересекаются под прямым углом.
Тетрагональная сингония. Два отрезка оси одинаковой длины пересекаются под прямым углом, третья ось перпендикулярна им, и отсекаемый на ней отрезок имеет иную длину.
Ромбическая сингония. Три оси разной длины пересекаются под прямыми углами.
Моноклинная сингония. Две оси разной длины пересекаются под косым углом, третья ось составляет с ними прямой угол.
Триклинная сингония. Три оси разной длины пересекаются под косыми углами.
Тригональная сингония. Три отрезка осей равной длины пересекаются в одной плоскости под углом 60o, третья ось перпендикулярна этой плоскости, и отсекаемый на ней отрезок имеет иную длину.
Гексагональная сингония. Положение осей аналогично их положению в тригональной сингонии.
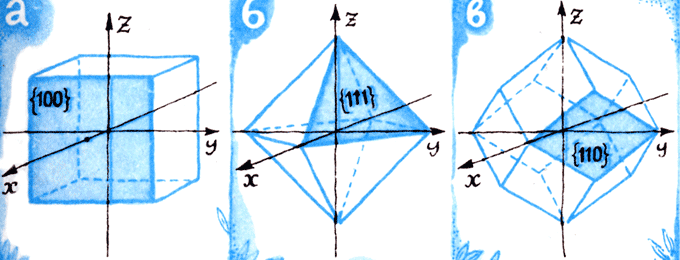
В самых симметричных кристаллах система координат получается прямоугольной, независимо от того, как поставить кристалл - по всем трем направлениям он развит совершенно одинаково - то есть имеет изометрический облик. Такие кристаллы относят к кубической сингонии. В них (и только в них) всегда имеются четыре оси L3. Простые формы - только закрытые: куб, октаэдр, тетраэдр и другие, иногда с большим числом граней. На кристаллах других сингонии эти простые формы не встречаются. В кубической сингонии кристаллизуются галит, пирит, флюорит, гранаты и много других минералов.
В тетрагональной сингонии оси также располагаются под прямыми углами, но по вертикальной оси кристалл развит иначе, чем по двум горизонтальным. Из-за этого остается только одна вертикальная ось симметрии L4 (а в кубическом кристалле оси L4 совпадают со всеми тремя координатными осями). Простые формы - тетрагональные призмы, пирамида, дипира-мида, пинакоид, моноэдр и др. Грани пинакоида и моноэдра перпендикулярны оси L4; иное их расположение привело бы к тому, что эта ось перестала "работать". Примеры тетрагональных кристаллов - рутил, циркон, везувиан, халькопирит. Найдите чертежи этих кристаллов и убедитесь, что они действительно относятся к тетрагональной сингонии.
В ромбической сингонии кристаллы развиты по-разному уже во всех трех направлениях. Вследствие этого здесь сохраняются оси симметрии только 2-го порядка. Простые формы - ромбические призмы, пирамиды, дипирамиды, отличающиеся от тетрагональных тем, что несколько растянуты в поперечном направлении и лишились из-за этого оси симметрии 4-го порядка. Пинакоид может располагаться либо перпендикулярно, либо параллельно продольной оси кристалла. Представители - оливин, барит, сера и др.
Есть и такие кристаллы, форма которых заставляет отказаться от прямоугольной системы координат. В моноклинной сингонии вследствие перекоса кристалла один из координатных углов получается не прямым. Здесь набор элементов симметрии еще беднее: либо единственная ось L2, либо плоскость симметрии, либо ось и плоскость, перпендикулярные друг другу (на их пересечении получается центр симметрии). Простые формы - пинакоид, ромбическая призма, диэдр, моноэдр. Примеры: ортоклаз, диопсид, гипс.
В кристаллах триклинной сингонии все координатные углы не прямые. Элементы симметрии отсутствуют вовсе либо имеется лишь один центр симметрии. Простые формы - моноэдры и пинакоиды. Примеры триклинных минералов - аксинит, халькантит, альбит.
Особняком стоят кристаллы, в которых главная ось симметрии имеет 3-й или 6-й порядок. Для них удобна 4-осная координатная система: три оси лежат в горизонтальной плоскости под углами 120o друг к другу, а четвертая перпендикулярна им и совпадает с единственной осью L3 (тригональная сингония) или L6 (гексагональная сингония). Простые формы гексагональной сингонии - гексагональные призма, пирамида и дипирамида, моноэдр и пинакоид (перпендикулярные L6). В тригональной сингонии к ним добавляются различные ромбоэдры и скаленоэдры и тригональные призмы, пирамида и дипирамида. В тригональной сингонии кристаллизуются, например, кварц, кальцит, гематит, турмалин; в гексагональной - апатит, берилл, молибденит, обычный лед (снежинки) и др.
Сингония - важная характеристика, имеющая большое значение, в частности, для определения неизвестных минералов. В каждой сингонии имеются свои особенности внешнего облика кристаллов и свой набор "руководящих" элементов симметрии. Уяснение этих особенностей на первых порах дается не без труда (особенно для гуманитариев и лиц с неполным средним образованием).
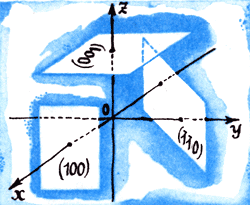 Используем системы координат, чтобы обозначить положение граней кристаллов. Это положение определяется углами, а не расстояниями. Назовем ось, направленную в сторону наблюдателя - Ох, вправо - Оу, вверх Oz. Идущие в этих направлениях значения на оси являются положительными, противоположные - отрицательными. Это обычное умолчание, принятое в элементарной математике. Каждую грань обозначают символом - заключенными в скобки числами (индексами). Индексы граней кристаллов - всегда целые и обычно небольшие числа. Больший индекс имеет та грань, которая составляет с данной осью больший угол.
Используем системы координат, чтобы обозначить положение граней кристаллов. Это положение определяется углами, а не расстояниями. Назовем ось, направленную в сторону наблюдателя - Ох, вправо - Оу, вверх Oz. Идущие в этих направлениях значения на оси являются положительными, противоположные - отрицательными. Это обычное умолчание, принятое в элементарной математике. Каждую грань обозначают символом - заключенными в скобки числами (индексами). Индексы граней кристаллов - всегда целые и обычно небольшие числа. Больший индекс имеет та грань, которая составляет с данной осью больший угол.
Если грань параллельна какой-нибудь оси, то ее индекс по этой оси равен нулю. Пересечение грани с отрицательной частью оси обозначается минусом над соответствующим индексом. Так, символ (100) означает, что грань пересекает ось Ох в ее передней (положительной) части и параллельна координатной плоскости yOz; грань (001) пересекает ось Oz и параллельна плоскости хОу; грань (110) пересекает ось Ох сзади и ось Оу спереди и параллельна оси Oz.
Аналогично обозначаются и простые формы кристаллов. Символом простой формы служит заключенный в фигурные скобки символ ее ближайшей к наблюдателю грани, расположенной в передней верхней части координатной системы. Например, в кубической сингонии символ куба {100}, октаэдра {111}, ромбододекаэдра {110}. На тетрагональном кристалле, имеющем грань {100}, вследствие симметрии L4 должны быть также грани {010}, {100} и {010}; в совокупности они образуют тетрагональную призму {100}, но не куб, так как для этого понадобилось бы "размножить" грань {100} еще двумя осями 4-го порядка, а их в кристаллах тетрагональной сингонии нет. Итак, один и тот же символ может обозначать в разных сингониях различные формы. Возможные пинакоиды: в тетрагональной сингонии {001}; в ромбической, моноклинной и триклинной {001}, {010} и {100}; в тригональной и гексагональной сингонии с четырмя осями {0001}. На самом деле четвертая ось в трехмерном пространстве является зависимой от трех остальных осей, и вводится четвертая ось исключительно для удобства описания кристалла, а не обозначения его четырехмерности (кристалл все равно продолжает оставаться трехмерным).
Перенося главные (самые большие и наилучшим образом выраженные) грани параллельно самим себе и продолжая их до пересечения друг с другом (с точки зрения закона постоянства углов это не вызывает возражений и описывается понятием подобия), мы всегда сможем из реального кристалла получить его собственную кристаллографическую идеальную модель кристалла.
