Рост кристаллов и кристаллические решетки, симметрия кристаллов
- Как растут кристаллы, математическая модель физического процесса new!!
- Внутренняя геометрия кристаллов, глава из Физики сплошных сред
- Рост кристаллов и кристаллические решетки, симметрия кристаллов
- Дислокация и рост кристаллов, физические модели роста кристаллов
§ 3. Рост кристаллов
Попробуйте представить себе образование кристаллов на Земле в естественных условиях. В поверхностном слое Земли все сорта атомов перемешаны между собой. Вулканическая деятельность, ветер и вода постоянно их смешивают, и они то и дело взбалтываются и перемешиваются. Но, несмотря на это, каким-то чудом атомы кремния постепенно начинают отыскивать друг друга, а потом и атомы кислорода, чтобы образовать вместе кремнезем. К одним атомам поодиночке пристраиваются другие, образуя кристалл, и смесь разделяется. А где-нибудь по соседству атомы хлора и натрия находят друг друга и строят кристалл соли.
Как же получается, что кристалл, начав строиться, позволяет присоединяться к себе только определенному сорту атомов? Так происходит потому, что вся система в целом стремится к наименьшему возможному значению энергии. Растущий кристалл примет новый атом, если благодаря ему энергия станет наименьшей. Но откуда кристалл знает, что атом кремния (или кислорода), будучи поставлен в данное место, приведет к наименьшему значению энергии? Узнает он это методом проб и ошибок. В жидкости и газе все атомы находятся в непрестанном движении.
Каждый атом ударяется об соседние примерно 1013 раз в секунду (в жидкости, при нормальных температурных условиях и давлении 1 атм.). Если атом ударяется о подходящее место в растущем кристалле, вероятность того, что он улетит обратно, будет меньше там, где меньше энергия. Продолжая так пробовать миллионы лет, с частотой около 1013 проб в секунду, атомы постепенно оседают на тех местах, где находят для себя положение с наименьшей энергией. В конце концов из них вырастают большие кристаллы.
§ 4. Кристаллические решетки
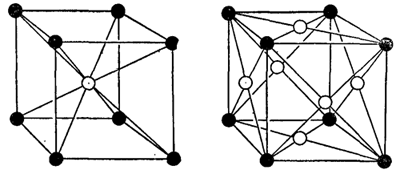
Расположение атомов в кристалле - кристаллическая решетка - может принимать множество геометрических форм. Мы опишем сначала простейшие решетки, характерные для большинства металлов и инертных газов в твердом состоянии. Это кубические решетки, которые могут быть двух видов: объемноцентрированная кубическая (рис. 30.4, а) и гранецентрированная кубическая (рис. 30.4, б). Конечно, на рисунках показан только один "куб" решетки; вы должны мысленно представить, что все это повторяется в трех измерениях до бесконечности. Для простоты на рисунке показаны только "центры" атомов. В настоящих кристаллах атомы скорее похожи на соприкасающиеся друг с другом шарики. Темные и светлые шарики на приведенных рисунках могут, вообще говоря, означать либо разные, либо одинаковые сорта атомов. Так, железо имеет объемноцентрированную кубическую решетку при низких температурах и гранецентрированную кубическую решетку при более высоких температурах. Физические свойства этих двух кристаллических форм совершенно различны.
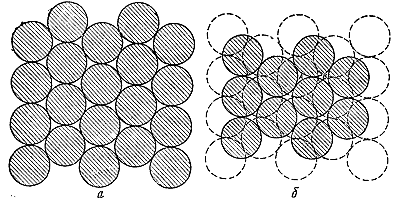
Но как возникают такие формы? Представьте, что вы должны как можно плотнее упаковать атомы - шарики. Можно было бы начать со слоя, где шарики уложены в "гексагональной плотной упаковке", как показано на рис. 30.5, а. Затем можно построить второй слой наподобие первого, но сместив его в горизонтальном направлении, как показано на рис. 30.5, б. А потом можно наложить и третий слой. Вот тут - внимание! Третий слой можно наложить двумя разными способами. Если вы начнете класть третий слой, помещая атом в точку А на рис. 30.5, б, то каждый атом в третьем слое окажется прямо над атомом первого нижнего слоя. Если же начать класть третий слой, помещая атом в точку В, то атомы третьего слоя будут расположены как раз над центрами треугольников, образованных тремя атомами нижнего о слоя. Любая другая начальная точка эквивалентна А или В, так что существует только два способа размещения третьего слоя.
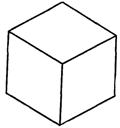 Если третий слой имеет атом в точке В, кристаллическая решетка будет гранецентрированной кубической, но видно это под некоторым углом. Забавно, что, начав с шестиугольников, можно прийти к кубической структуре. Но обратите внимание, что куб, рассматриваемый под определенным углом, имеет очертания шестиугольника. Например, рис. 30.6 может изображать либо плоский шестиугольник, либо и куб в перспективе (справа).
Если третий слой имеет атом в точке В, кристаллическая решетка будет гранецентрированной кубической, но видно это под некоторым углом. Забавно, что, начав с шестиугольников, можно прийти к кубической структуре. Но обратите внимание, что куб, рассматриваемый под определенным углом, имеет очертания шестиугольника. Например, рис. 30.6 может изображать либо плоский шестиугольник, либо и куб в перспективе (справа).
Если к рис. 30.5, б добавляется третий слой, начиная с атома в точке А, то кубической структуры не возникает и у решетки будет только гексагональная симметрия. Ясно, что обе описанные нами возможности дают одинаковую плотную упаковку. Некоторые металлы (например, серебро и медь) выбирают первую альтернативу - решетка у них гранецентрированная кубическая. Другие же (например, бериллий и магний) предпочитают вторую возможность и образуют гексагональные кристаллы. Очевидно, появление той или иной решетки не может зависеть только от способа упаковки маленьких шариков, но должно еще определяться и другими факторами. В частности, оказывается существенной небольшая угловая зависимость межатомных сил (или в случае металлов от энергии электронного океана). Все эти вещи Вы легко узнаете из традиционного курса химии.
§ 5. Симметрии в двух измерениях
Теперь мне хотелось бы обсудить некоторые свойства кристаллов с точки зрения их внутренних симметрии. Основное свойство кристалла состоит в том, что если вы сдвинетесь от одного атома на один период решетки к соответствующему атому, то попадете в точно такое же окружение. Это фундаментальное утверждение. Но если бы вы сами были атомом, то могли бы заметить другое передвижение, которое привело бы вас в точно такое же окружение, т. е. в другую возможную "симметрию". На рис. 30.7, а показан еще один возможный узор обоев (хотя вы, наверно, такого никогда не видали). Предположим, что мы сравниваем окружения в точках А и В. Вы могли бы сперва подумать, что они одинаковы. Не совсем. Точки С и D эквивалентны А, но окружение В подобно А, только если все рядом обращать как будто в зеркале.
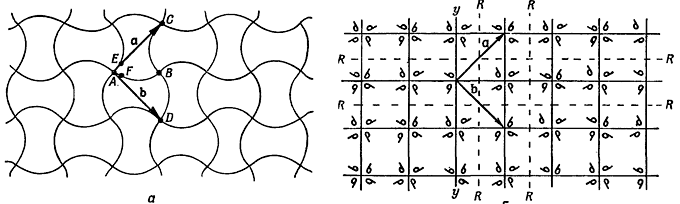
В этом узоре имеются еще и другие виды "эквивалентных" точек. Так, точки Е и F обладают "одинаковыми" окружениями, за тем исключением, что одно повернуто на 90o по отношению к другому. Узор особенный. Вращение на 90o, проделанное сколько угодно раз вокруг такой вершины, как А, снова дает тот же узор. Кристалл с такой структурой имел бы на поверхности прямые углы, но внутри он устроен сложнее, чем простой куб. Теперь, когда мы описали ряд частных случаев, попытаемся вывести все возможные типы симметрии, какие может иметь кристалл. Прежде всего посмотрим, что получается в плоскости. Плоская решетка может быть определена с помощью двух так называемых основных векторов, которые идут от одной точки решетки к двум ближайшим эквивалентным точкам. Два вектора 1 и 2 суть основные векторы решетки на рис. 30.1. Два вектора а и b на рис. 30.7, а - основные векторы для изображенного там узора. Мы могли бы, конечно, с тем же успехом заменить а на -а или b на -b. Раз а и b одинаковы по величине и перпендикулярны друг другу, то вращение на 90o переводит в себя и снова дает ту же решетку.
Итак, мы видим, что существуют решетки, обладающие "четырехсторонней" симметрией. А раньше мы описали плотную упаковку, основанную на шестиугольнике и обладающую шестисторонней симметрией. Вращение набора кружков на рис. 30.5, а на угол 60o вокруг центра любого шарика переводит рисунок сам в себя.
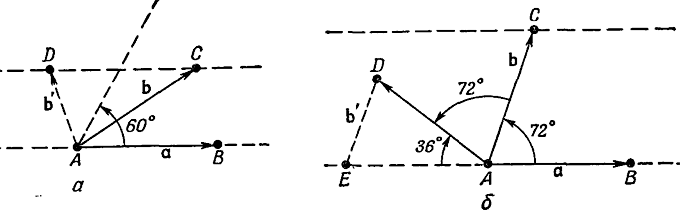
Какие виды вращательной симметрии существуют еще? Может ли быть, например, вращательная симметрия пятого или восьмого порядка? Легко понять, что они невозможны. Единственная симметрия, связанная с фигурой, имеющей более четырех сторон, есть симметрия шестого порядка. Прежде всего покажем, что симметрия более чем шестого порядка невозможна. Попытаемся вообразить решетку с двумя равными основными векторами, образующими угол менее 60 (рис. 30.8, а). Мы должны предположить, что точки В и С эквивалентны А и что а и b - наиболее короткие векторы, проведенные из А до эквивалентных соседей. Но это, безусловно, неверно, потому что расстояние между В и С короче, чем от любого из них до А. Должна существовать соседняя точка D, эквивалентная А, которая ближе к А, чем к В или С. Мы должны были бы выбрать B в качестве одного из основных векторов. Поэтому угол между основными векторами должен быть равен 60o или еще больше. Октагональная симметрия невозможна.
А как быть с пятикратной симметрией? Если мы предположим, что основные векторы а и b имеют одинаковую длину и образуют угол 72o (рис. 30.8, б), то должна существовать эквивалентная точка решетки в D под 72o к линии АС. Но вектор b от Е к D тогда короче b, и b уже не основной вектор. Пятикратной симметрии быть не может. Единственные возможности, не приводящие к подобным трудностям, это 9 = 60, 90 или 120o. Очевидно, допустимы также нуль и 180o. Можно еще так выразить полученный нами результат: рисунок может не меняться при повороте на полный оборот (ничего не изменяется), полоборота, одну треть, одну четверть или одну шестую оборота. И этим исчерпываются все возможные вращательные симметрии на плоскости - всего их пять. Если n, то мы говорим об "n-кратной" симметрии, или симметрии ге-го порядка. Мы говорим, что узор, для которого n равно 4 или 6, обладает более "высокой симметрией", чем узор с n, равным 1 или 2.
Вернемся к рис. 30.7, а. Мы видим, что узор там обладает четырехкратной вращательной симметрией. На рис. 30.7,б мы нарисовали другое расположение, которое обладает теми же свойствами симметрии, что и рис. 30.7,а. Маленькие фигурки, похожие на запятые, - это асимметричные объекты, которые служат для определения симметрии изображения внутри каждого квадратика. Заметьте, что запятые в соседних квадратиках перевернуты попеременно, так что элементарная ячейка больше одного квадратика. Если бы запятых не было, рисунок по-прежнему обладал бы четырехкратной симметрией, но элементарная ячейка была бы меньше. Посмотрим внимательно на рис. 30.7; мы обнаружим, что они обладают еще и другими типами симметрии. Так, отражение относительно каждой пунктирной линии R-R воспроизводит рисунок без изменений. Но это еще не все. У них есть еще один тип симметрии. Если отразить рисунок относительно линии R-R, а затем сдвинуть на один квадратик вправо (или влево), то снова получится первоначальный рисунок. Линия R-R называется линией скольжения.
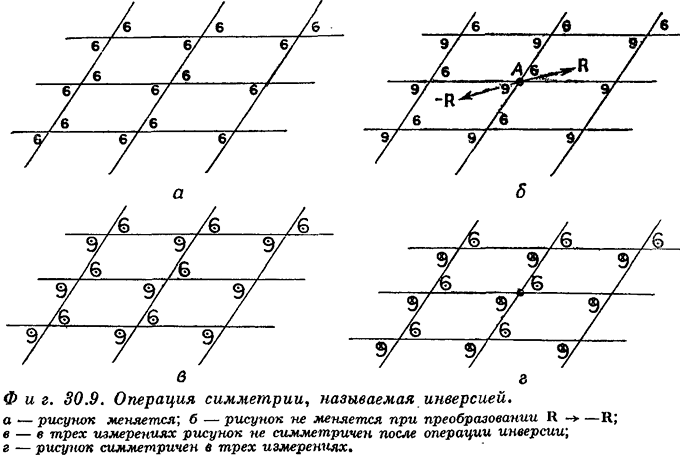
Этим исчерпываются все типы симметрии в пространстве двух измерений. Есть еще одна пространственная операция симметрии, которая на плоскости эквивалентна вращению на 180o, однако в трехмерном пространстве она не сводится к этому вращению, а есть совсем другая операция. Я говорю об инверсии. Под инверсией мы подразумеваем такую операцию, когда любая точка, отвечающая вектору смещения из начала координат R (например, точка А на рис. 30.9, б), переносится в точку -R.
Инверсия рисунка а на рис. 30.9 дает новый рисунок, а инверсия рисунка б приводит к такому же рисунку. На двумерном узоре (вы можете это видеть) инверсия рисунка б в точке А эквивалентна повороту на 180o вокруг той же самой точки. Предположим, однако, что мы сделали узор на рис. 30.9, б трехмерным, вообразив на маленьких шестерках и девятках "стрелочки", смотрящие из страницы кверху. В результате инверсии в трехмерном пространстве все стрелочки перевернутся и направятся вниз, так что узор не воспроизведется. Если мы обозначим острия и хвосты стрелок точками и крестиками, то сможем образовать трехмерный рисунок (рис. 30.9, в), который несимметричен относительно инверсии, или же мы можем получить рисунок, который такой симметрией обладает (рис. 30.9, г). Заметьте, что трехмерную инверсию нельзя получить никакой комбинацией вращений.
Если мы будем характеризовать "симметрию" рисунка (или решетки) разного рода операциями симметрии, которые мы только что описали, то окажется, что в двумерном случае существуют 17 различных форм узоров. Узор с наинизшей возможной симметрией мы изобразили на рис. 30.1, а узор с одной из наивысших симметрии - на рис. 30.7.
Удивительно, как мало типов из этих 17 используется при изготовлении обоев и тканей! Всегда видишь одни и те же три или четыре основных типа. В чем здесь дело? Неужели так убога фантазия художников и дизайнеров или, может быть, многие из возможных типов рисунков не будут так радовать глаз?
§ 6. Симметрии в трех измерениях
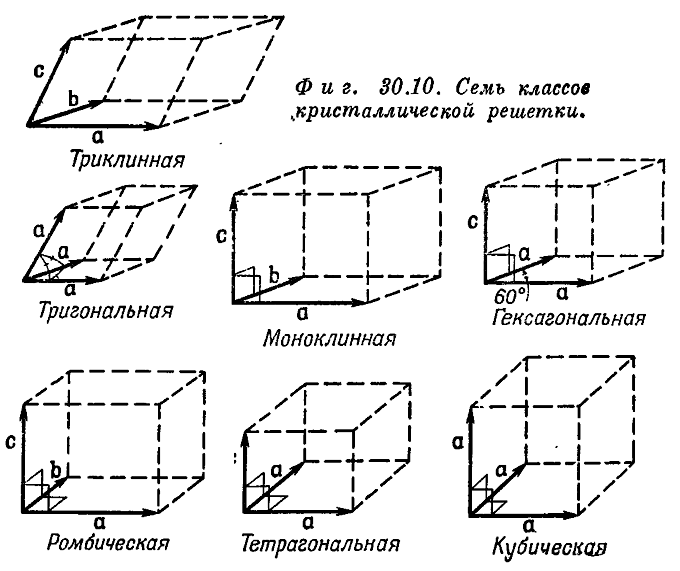
До сих пор мы говорили только об узорах в двух измерениях. На самом же деле нас интересуют способы размещения атомов в трех измерениях. Прежде всего очевидно, что трехмерный кристалл имеет три основных вектора. Если же мы поинтересуемся возможными операциями симметрии в трех измерениях, то обнаружим, что существует 230 возможных типов симметрии! По некоторым соображениям, эти 230 типов можно разделить на семь классов, представленных на рис. 30.10. Решетка с наименьшей симметрией называется триклинной.
Ее элементарная ячейка представляет собой параллелепипед. Основные векторы все имеют разную длину и нет ни одной одинаковой пары углов между ними. И никакой вращательной или зеркальной симметрии здесь нет. Однако есть еще одна операция: при инверсии в узле элементарная ячейка может меняться, а может и не меняться. [Под инверсией в трех измерениях мы снова подразумеваем, что пространственное смещение R заменяется на -R, или, другими словами, точка с координатами (х, у, z) переходит в точку с координатами (-х, -у, -z). Поэтому симметрия триклинной решетки может быть только двух типов - с центром инверсии и без него.] Пока мы считали, что все векторы разные и расположены под произвольными углами. Если же все векторы одинаковы и углы между ними равны, то получается тригональная решетка, изображенная на рисунке. Ячейка такой решетки может иметь добавочную симметрию; она может еще и не меняться при вращении вокруг наибольшей диагонали.
Если один из основных векторов, скажем с, направлен под прямым углом к двум остальным, то мы получаем моноклинную элементарную ячейку. Здесь возможна новая симметрия - вращение на 180o вокруг с. Гексагональная решетка - это частный случай, когда векторы а и b равны и угол между ними составляет 60o, так что вращение на 60, 120 или 180o вокруг вектора с приводит к той же самой решетке (для определенных внутренних типов симметрии).
Если все три основных вектора перпендикулярны друг другу, но не равны по длине, получается ромбическая ячейка. Фигура симметрична относительно вращений на 180o вокруг трех осей. Типы симметрии более высокого порядка возникают у тетрагональной ячейки, все углы которой прямые и два основных вектора равны. Наконец, имеется еще кубическая ячейка, самая симметричная из всех.
Основной смысл всего этого разговора о типах симметрии состоит в том, что внутренняя симметрия кристалла проявляется (иногда весьма тонким образом) в макроскопических физических свойствах кристалла. В гл. 31 мы увидим, например, что электрическая поляризуемость кристалла, вообще говоря, представляет собой тензор. Если описывать тензор в терминах эллипсоида поляризуемости, то мы должны доказать, что некоторые типы симметрии кристалла проявятся в этом эллипсоиде. Так, кубический кристалл симметричен по отношению к вращению на 90o вокруг любого из трех взаимно перпендикулярных направлений. Единственный эллипсоид с таким свойством, очевидно, сфера. Кубический кристалл должен быть изотропным диэлектриком.
С другой стороны, тетрагональный кристалл обладает вращательной симметрией четвертого порядка. Две главные оси его эллипсоида должны быть равны, а третья должна быть параллельна оси кристалла. Аналогично, поскольку ромбический кристалл обладает вращательной симметрией второго порядка относительно трех перпендикулярных осей, его оси должны совпадать с осями эллипсоида поляризуемости. Точно так же одна из осей моноклинного кристалла должна быть параллельна одной из главных осей эллипсоида, хотя о других осях мы ничего сказать не можем. Триклинный кристалл не обладает вращательной симметрией, поэтому его эллипсоид может иметь любую ориентацию.
Как видите, мы можем с пользой провести время, придумывая всевозможные типы симметрии и связывая их со всевозможными физическими тензорами. Мы рассмотрели только тензор поляризуемости, здесь дело было простое, а для других тензоров, например для тензора упругости, рассуждать будет труднее. Существует раздел математики, называемый "теорией групп", который занимается такими вещами, но обычно можно сообразить все, что нужно, опираясь лишь на здравый смысл.
